Python でチェビシェフ(Chebyshev)基底を使った高次の多項式近似
こんにちは。
仕事の自動化にやりがいと達成感を感じるガッくんです。
この記事の目次
背景・目的
前回の記事で polyfit で多項式近似をやりました。
Python で多項式近似と決定係数 - 解析エンジニアの自動化 blog
近似曲線を作る際になかなか便利なものができたと思います。
しかし、高次の多項式近似で Warning が出ていました。。
調べていくとチェビシェフ(Chebyshev)基底を使った多項式近似という方法が高次の曲線でも安定的に近似曲線が得られるらしいことが分かりました。
テスト用にある程度複雑な波形を作り、 誤差を与えます。
そして、誤差を含む波形上の点に対して近似曲線を作ります。
動作環境
・Windows 7
・winpython 64bit 3.4.4
プログラム
ソースコード
###############################################################################
# チェビシェフ基底多項式近似
###############################################################################
#==============================================================================
# ファイルインポート
#==============================================================================
import numpy as np
import matplotlib.pyplot as plt
from numpy.polynomial import Chebyshev as c
#==============================================================================
# グラフ描画関数
#==============================================================================
def wave_graph(x, y, x1, y1, xmin, xmax, ymin, ymax):
plt.figure(figsize=(8, 6))
# 元々の値の出力
plt.plot(x, y, 'r.', label="original data point")
plt.plot(x, y, 'r')
# 誤差を含んだ値の出力
plt.plot(x1, y1, 'b.', label="data point for test")
plt.plot(x1, y1, 'b')
# グラフのタイトル・目盛設定
plt.title("wave for test")
plt.xlim([xmin, xmax])
plt.ylim([ymin, ymax])
# 凡例の位置設定
plt.legend(loc='upper right')
# 格子の設定
plt.grid(which='major', color='black', linestyle='-')
plt.grid(which='minor', color='black', linestyle='-')
# グラフ出力
file_name = 'wave for test.jpg'
plt.savefig(file_name)
# 表示
plt.show()
return file_name
def err_graph(x, y, xmin, xmax, ymin, ymax):
plt.figure(figsize=(8, 6))
# 各 x 値における誤差の出力
plt.bar(x, y, linewidth = 0, width = 0.0007, color="#1E7F00")
plt.plot(x, y, 'r.', label="error of data point")
plt.plot(x, y, 'r')
# グラフのタイトル・目盛設定
plt.title("error of wave for test")
plt.xlim([xmin, xmax])
plt.ylim([ymin, ymax])
# 凡例の位置設定
plt.legend(loc='upper right')
# 誤差の表示
max_err = max(y)
min_err = min(y)
plt.text(xmin+np.abs((xmax-xmin)*0.01), ymin+np.abs((ymax-ymin)*0.07), 'upper error = ' + str(max_err))
plt.text(xmin+np.abs((xmax-xmin)*0.01), ymin+np.abs((ymax-ymin)*0.01), 'lower error = ' + str(min_err))
# 格子の設定
plt.grid(which='major', color='black', linestyle='-')
plt.grid(which='minor', color='black', linestyle='-')
# グラフ出力
file_name = 'error of wave for test.jpg'
plt.savefig(file_name)
# 表示
plt.show()
return file_name
def graph(x, y, a, b, interpolation_method):
plt.figure(figsize=(8, 6))
# 元々の値の出力
plt.plot(x, y, 'ro', label="data point")
# 補間した結果を出力
plt.plot(a, b, 'k', label=interpolation_method)
# グラフのタイトル・目盛設定
plt.title(interpolation_method)
plt.grid(True)
plt.xlabel('time[sec]')
plt.ylabel('amplitude')
# 凡例の位置設定
plt.legend(loc='lower right')
# グラフ出力
file_name = interpolation_method + '.jpg'
plt.savefig(file_name)
# 表示
plt.show()
#==============================================================================
# チェビシェフ基底を使った多項式近似関数
#==============================================================================
def chebyshev(x, y, stop_n, point):
X = np.linspace(x[0], x[-1], num=point, endpoint=True) # x の値の準備
max_corrcoef = 0 # 最終的に採用した決定係数記憶用変数
orders = [] # 次数の履歴記憶用変数
corrcoefs = [] # 決定係数の履歴記憶用変数
eps = 0.00001 # 打切り誤差
for n in range(1, stop_n): # 1 ~ stop_n まで繰り返す
f = c.fit(x, y, n) # 多項式近似
Y = f(X) # X に対応する y の値を計算する
corrcoef = np.corrcoef(y, f(x))[0, 1]**2 # 決定係数を計算する
orders.append(n) # 次数の履歴記憶
corrcoefs.append(corrcoef) # 決定係数の履歴記憶
# 現状最大の決定係数 max_corrcoef とさっき計算した corrcoef の差の絶対値が打切り誤差より小さい場合
if abs(max_corrcoef - corrcoef) < eps:
break # 多項式計算のループ終了
# 現状最大の決定係数 max_corrcoef よりさっき計算した corrcoef が大きい場合
if max_corrcoef < corrcoef:
max_corrcoef = corrcoef # max_corrcoef の更新
fix_Y = Y # 最大決定係数の時の Y を記憶する
fix_n = n # 最大決定係数を記憶する
plt.figure(figsize=(8, 6)) # グラフの初期化
plt.plot(orders, corrcoefs, 'r.', label="coefficient of determination") # 決定係数の値の出力
plt.plot(orders, corrcoefs, 'r') # 値のドットを線で結ぶ
plt.legend(loc='lower right') # 凡例の位置設定
plt.grid(True) # 罫線表示
plt.xlabel('order') # 横軸タイトル
plt.ylabel('coefficient of determination') # 縦軸タイトル
file_name = 'Determination coefficient transition to ' + str(n) + '.jpg' # グラフ名設定
plt.savefig(file_name) # グラフ出力
return X, fix_Y, fix_n
#==============================================================================
# 決定係数が最大を示す n 次式の最小二乗法近似関数
#==============================================================================
def n_th_order_least_squares_approximation_by_max_corrcoef(x, y, stop_n, point):
X = np.linspace(x[0], x[-1], num=point, endpoint=True) # x の値の準備
max_corrcoef = 0 # 最終的に採用した決定係数記憶用変数
orders = [] # 次数の履歴記憶用変数
corrcoefs = [] # 決定係数の履歴記憶用変数
for n in range(1, stop_n): # 1 ~ stop_n まで繰り返す
f = np.poly1d(np.polyfit(x, y, n)) # 多項式近似
Y = f(X) # X に対応する y の値を計算する
corrcoef = np.corrcoef(y, f(x))[0, 1]**2 # 決定係数を計算する
orders.append(n) # 次数の履歴記憶
corrcoefs.append(corrcoef) # 決定係数の履歴記憶
# 現状最大の決定係数 max_corrcoef よりさっき計算した corrcoef が大きい場合
if max_corrcoef < corrcoef:
max_corrcoef = corrcoef # max_corrcoef の更新
fix_Y = Y # 最大決定係数の時の Y を記憶する
fix_n = n # 最大決定係数を記憶する
plt.figure(figsize=(8, 6)) # グラフの初期化
plt.plot(orders, corrcoefs, 'r.', label="coefficient of determination") # 決定係数の値の出力
plt.plot(orders, corrcoefs, 'r') # 値のドットを線で結ぶ
plt.legend(loc='lower right') # 凡例の位置設定
plt.grid(True) # 罫線表示
plt.xlabel('order') # 横軸タイトル
plt.ylabel('coefficient of determination') # 縦軸タイトル
file_name = 'Determination coefficient transition to ' + str(fix_n) + '.jpg' # グラフ名設定
plt.savefig(file_name) # グラフ出力
return X, fix_Y, fix_n # 戻り値
#==============================================================================
# 決定係数が上昇しなくなった n 次式の最小二乗法近似関数
#==============================================================================
def n_th_order_least_squares_approximation_by_eps(x, y, stop_n, point):
X = np.linspace(x[0], x[-1], num=point, endpoint=True) # x の値の準備
max_corrcoef = 0 # 最終的に採用した決定係数記憶用変数
orders = [] # 次数の履歴記憶用変数
corrcoefs = [] # 決定係数の履歴記憶用変数
eps = 0.00001 # 打切り誤差
for n in range(1, stop_n): # 1 ~ stop_n まで繰り返す
f = np.poly1d(np.polyfit(x, y, n)) # 多項式近似
Y = f(X) # X に対応する y の値を計算する
corrcoef = np.corrcoef(y, f(x))[0, 1]**2 # 決定係数を計算する
orders.append(n) # 次数の履歴記憶
corrcoefs.append(corrcoef) # 決定係数の履歴記憶
# 現状最大の決定係数 max_corrcoef とさっき計算した corrcoef の差の絶対値が打切り誤差より小さい場合
if abs(max_corrcoef - corrcoef) < eps:
break # 多項式計算のループ終了
# 現状最大の決定係数 max_corrcoef よりさっき計算した corrcoef が大きい場合
if max_corrcoef < corrcoef:
max_corrcoef = corrcoef # max_corrcoef の更新
fix_Y = Y # 最大決定係数の時の Y を記憶する
fix_n = n # 最大決定係数を記憶する
plt.figure(figsize=(8, 6)) # グラフの初期化
plt.plot(orders, corrcoefs, 'r.', label="coefficient of determination") # 決定係数の値の出力
plt.plot(orders, corrcoefs, 'r') # 値のドットを線で結ぶ
plt.legend(loc='lower right') # 凡例の位置設定
plt.grid(True) # 罫線表示
plt.xlabel('order') # 横軸タイトル
plt.ylabel('coefficient of determination') # 縦軸タイトル
file_name = 'Determination coefficient transition to ' + str(fix_n) + '.jpg' # グラフ名設定
plt.savefig(file_name) # グラフ出力
return X, fix_Y, fix_n # 戻り値
#==============================================================================
# テスト用データ作成
#==============================================================================
# 値の準備 =====================================================================
N = 2**8 # サンプリング数
dt = 0.0009 # サンプリング周期
ampl = np.array([ 1, 1, 2, 1]) # 振幅
freq = np.array([ 10, 20, 30, 40]) # 周波数
peri_axis = np.arange(0, N*dt, dt) # 周期軸
error = 0.11 # 誤差係数
for i in range(len(freq)):
if i == 0:
origin_y = ampl[i] * np.sin(2*np.pi*freq[i]*peri_axis) # 入力波形
y = ampl[i] * np.sin(2*np.pi*freq[i]*peri_axis) + error * np.random.randn(N) # 誤差を与えた入力波形
else:
origin_y += ampl[i] * np.sin(2*np.pi*freq[i]*peri_axis) # 入力波形
y += ampl[i] * np.sin(2*np.pi*freq[i]*peri_axis) + error * np.random.randn(N) # 誤差を与えた入力波形
# 与えた誤差の計算 ==============================================================
err = (y) - (origin_y)
# グラフ出力設定 ================================================================
xmin = min(peri_axis) - (3*dt) # グラフの x 軸の最小値設定
xmax = max(peri_axis) + (3*dt) # グラフの x 軸の最大値設定
ymin = min(y) * 1.2 # グラフの y 軸の最小値設定
ymax = max(y) * 1.2 # グラフの y 軸の最大値設定
x_scale_interval = 1 # x 方向目盛間隔
y_scale_interval = 1 # y 方向目盛間隔
max_err = max(err)
min_err = min(err)
ymin_err = min_err * 1.5
ymax_err = max_err * 1.5
# グラフ出力 ====================================================================
wave_graph(peri_axis, origin_y, peri_axis, y, xmin, xmax, ymin, ymax)
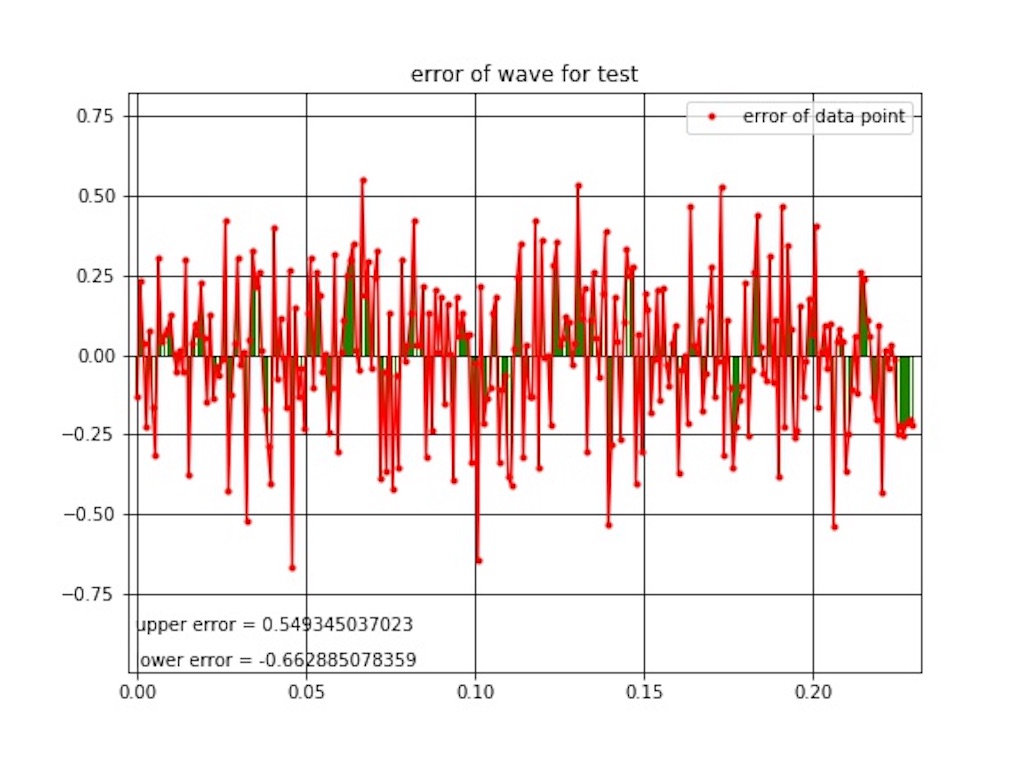
err_graph(peri_axis, err, xmin, xmax, ymin_err, ymax_err)
# 決定係数が最大を示す次数による多項式補間 =========================================
X, Y, n = n_th_order_least_squares_approximation_by_max_corrcoef(peri_axis, y, 200, 1000)
graph(peri_axis, origin_y, X, Y, str(n) + 'th order by max coef')
# 決定係数が上昇しなくなった次数による多項式補間 ======================================
X, Y, n = n_th_order_least_squares_approximation_by_eps(peri_axis, y, 200, 1000)
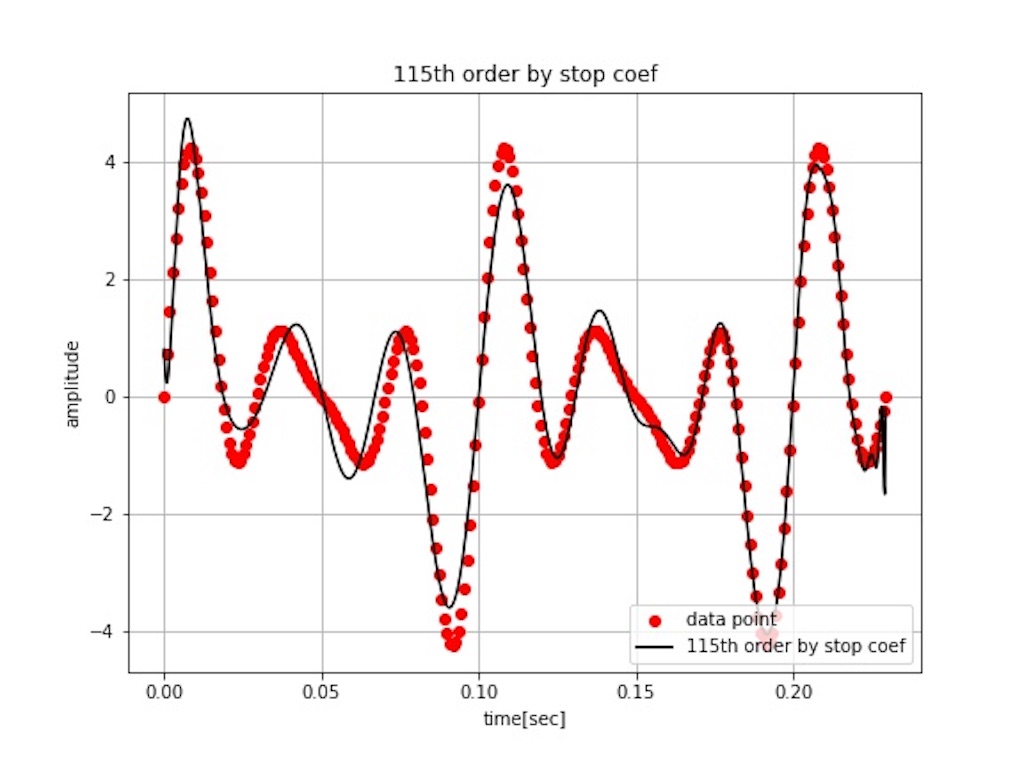
graph(peri_axis, origin_y, X, Y, str(n) + 'th order by stop coef')
# チェビシェフ基底を使った多項式近似 =================================================
X, Y, n = chebyshev(peri_axis, y, 200, 1000)
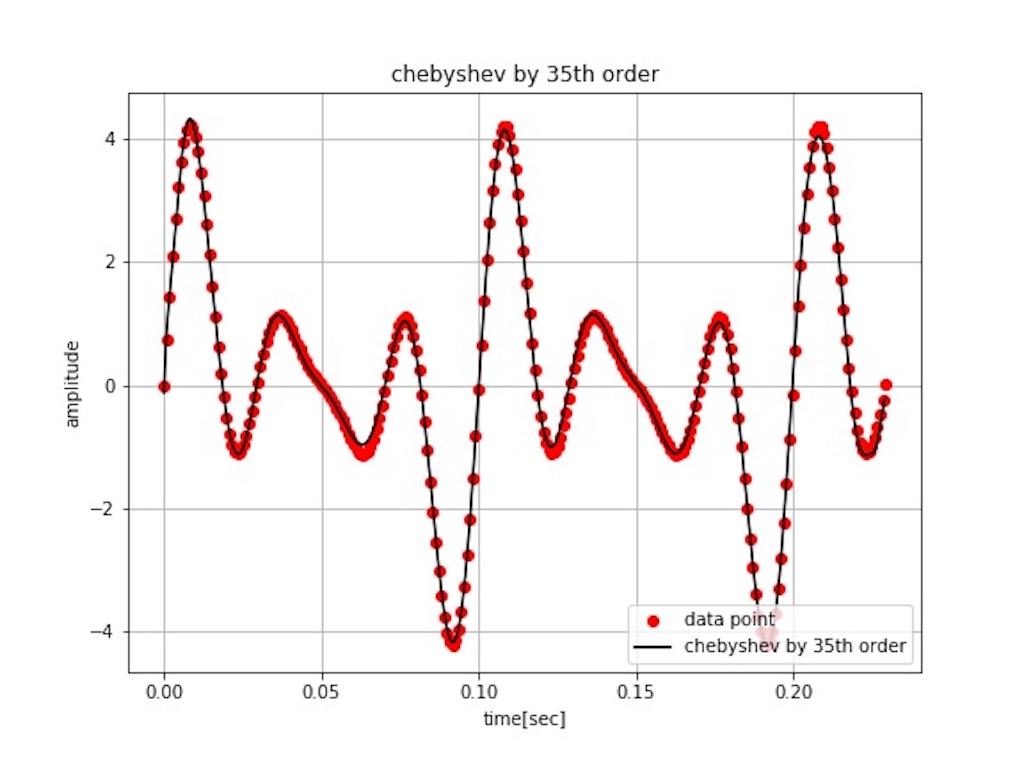
graph(peri_axis, origin_y, X, Y, 'chebyshev by ' + str(n) + 'th order')
結果
polyfit による多項式近似曲線は前回の記事で作成済みなので、流用して、チェビシェフ基底を使った多項式近似曲線と比較してみました。
具体的には下記の①〜③の近似曲線を作成して傾向を確認しました。
①決定係数が最大を示した次数の近似曲線
②決定係数の上昇が無くなった次数の近似曲線
③ 定係数の上昇が無くなった次数のチェビシェフ近似曲線

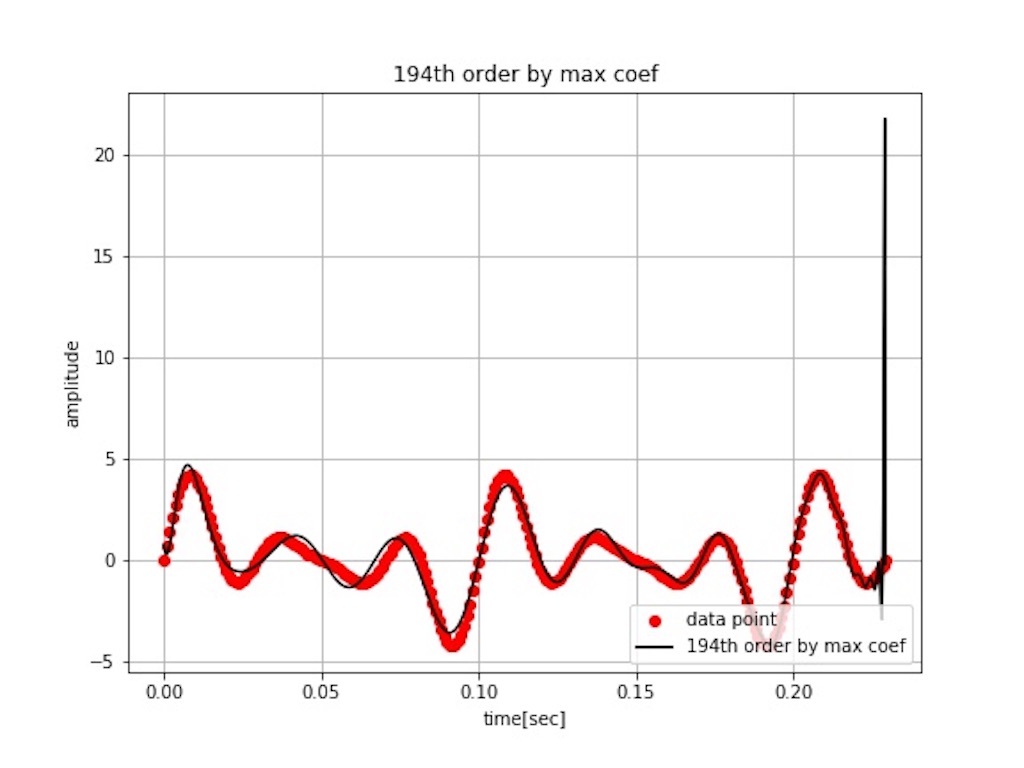
①の近似曲線は 194 次という大きな次数の近似曲線です。
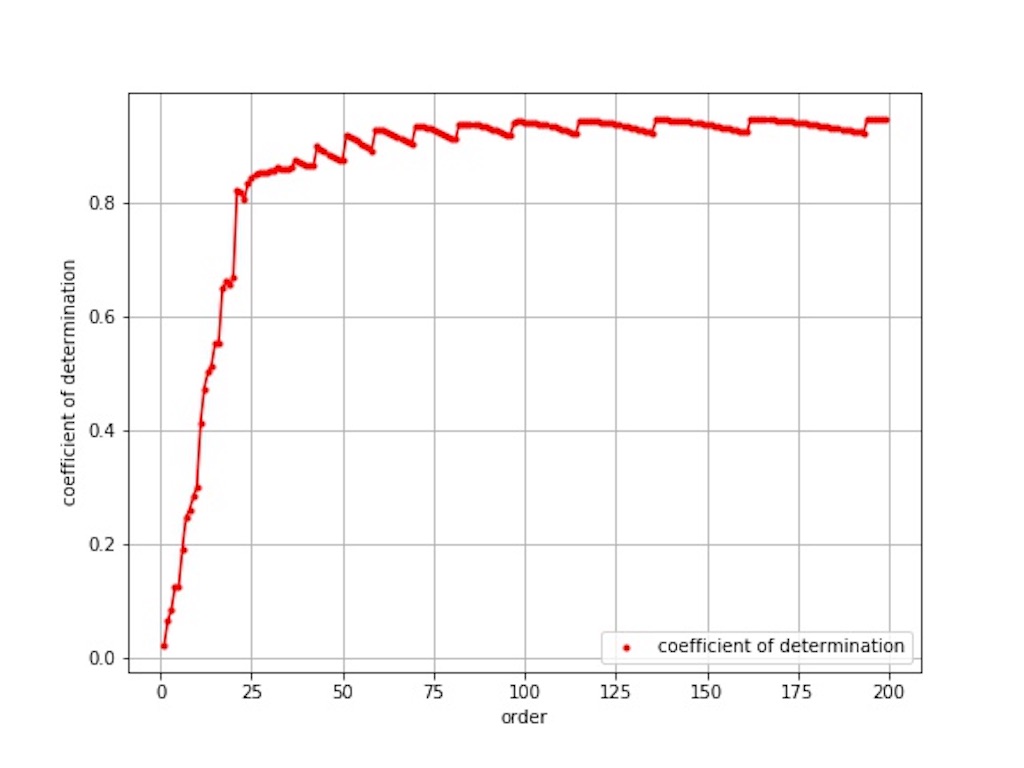
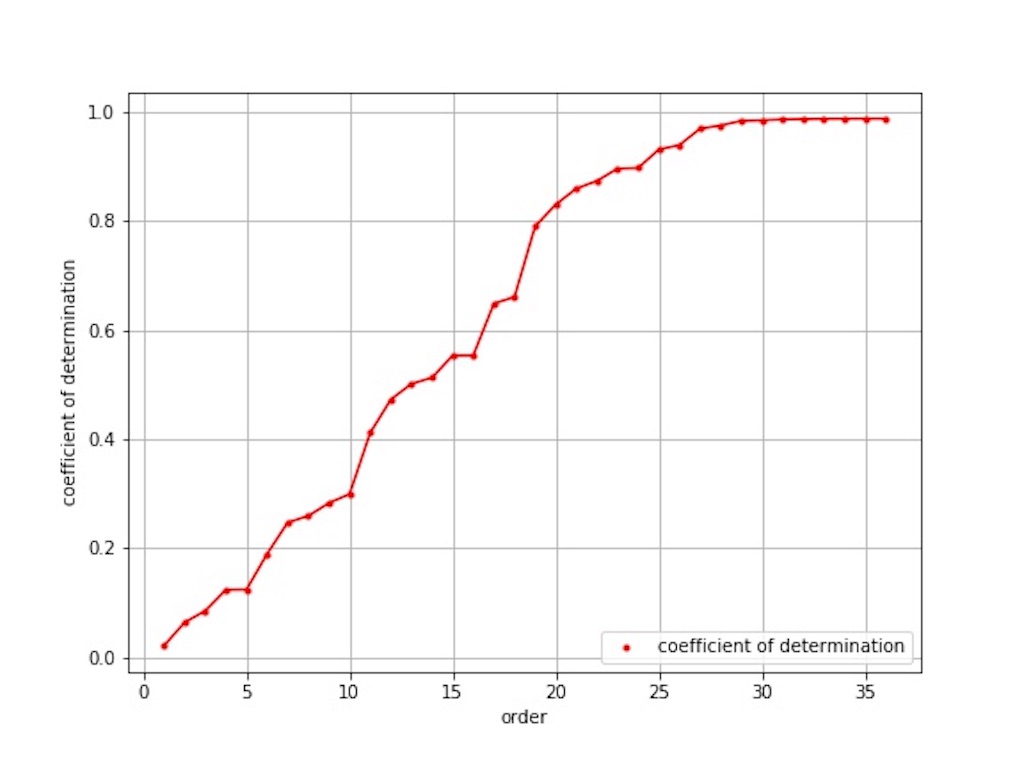
図3 から次数を上げるにつれて決定係数も上昇している傾向が分かります。
元々の波形が複雑なので決定係数が 1 付近に来る決定係数の傾向も乱れが生じています。
図4 は 0.24 秒あたりで波形が大きく乱れています。
決定係数は高いのですが、全く近似出来ていません。
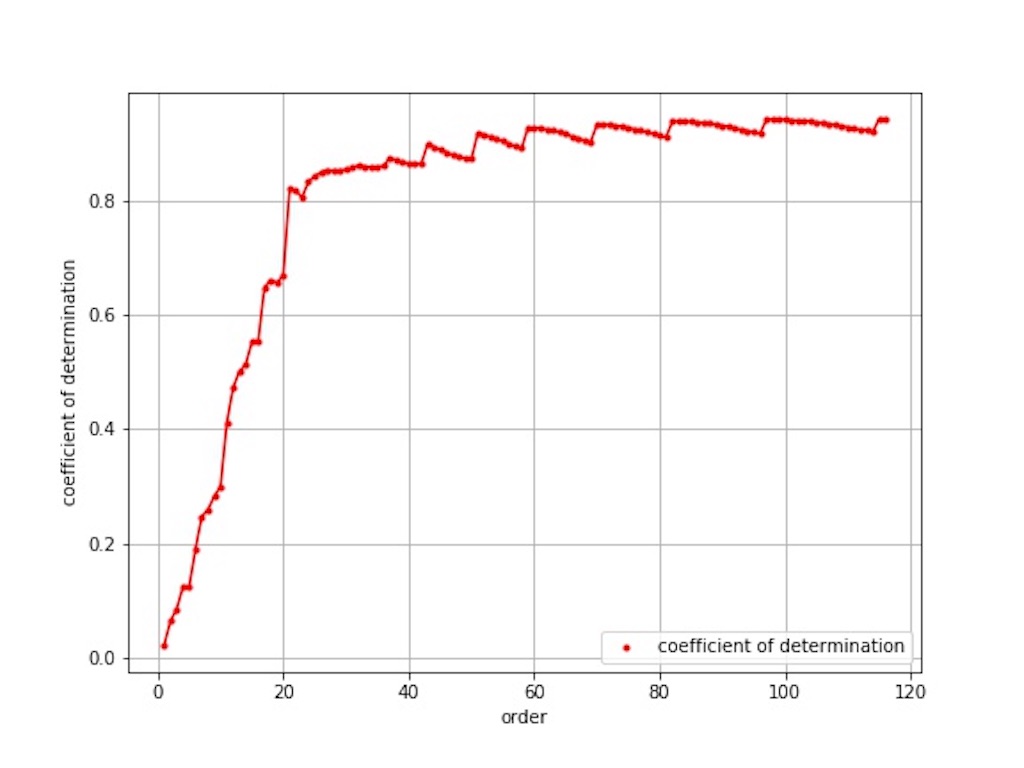
図5 を見ると決定係数がほぼ一定になる領域に達してすぐに終了しています。
図6 は図4 程は乱れが無いですが、近似精度は良くありません。
やはり、決定係数の値が 1 に近ければ良いのではなく、決定係数が上昇傾向から一定に移り変わる時の次数による近似曲線のほうが良く曲線を表現出来そうです。
図7 を見ると図3 、図5 とは違い、 1 に近い一定となる領域での乱れがありません。
図8 の近似曲線はかなり精度よく曲線を表現出来ています。
以上