Python で 放射基底関数 (RBF) 補間
こんにちは。
仕事の自動化にやりがいと達成感を感じるガッくんです。
この記事の目次
背景・目的
前の記事でスプライン曲線で曲線近似を試しました。近似というかほぼ補間ですが…
しかし、放射基底関数 (RBF) の補間を忘れていました。
しかも、 Scipy には放射基底関数 (RBF) の補間が関数として用意されているではありませんか‼︎
この補間方法は絶対記事にして残しておきたい‼︎
動作環境
・Windows 7
・winpython 64bit 3.4.4
プログラム
ソースコード
###############################################################################
# 放射基底関数補間プログラム
###############################################################################
#==============================================================================
# ライブラリインポート
#==============================================================================
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
#==============================================================================
# RBF 補間関数
#==============================================================================
def rbf2d(x, y, kernel):
# 線形 RBF => linear
# ガウシアン RBF => gaussian
# 多重二乗 RBF => multiquadric
# 逆二乗 RBF => inverse
# 多重調和スプライン RBF => cubic(3次), quintic(5次), thin_plate(薄板スプライン)
# RBF 関数の作成
rbf = interpolate.Rbf(x, y, function=kernel)
# 入力されている x 値の最小値から最大値の間で任意の間隔で分割する
xi = np.linspace(x.min(), x.max(), 314)
# xi に対応する yi を計算する
yi = rbf(xi)
# グラフ描画
plt.figure(figsize=(10, 8))
plt.plot( x, y, 'ro', label='original data point', markersize=4)
plt.plot(xi, yi, 'r', label='rbf - ' + kernel)
# 格子の設定
plt.xlim([xi.min(), xi.max()])
plt.ylim([yi.min()*1.3, yi.max()*1.3])
plt.grid(which='major', color='black', linestyle='-')
plt.grid(which='minor', color='black', linestyle='-')
plt.title("interpolate rbf - " + kernel)
plt.legend(loc='upper right') # 凡例の位置設定
# グラフ出力
file_name = "interpolate rbf - " + kernel + ".jpg"
plt.savefig(file_name)
plt.show()
#==============================================================================
# 重ね合わせグラフ描画関数
#==============================================================================
def graph(x, y):
# 線形 RBF => linear
# ガウシアン RBF => gaussian
# 多重二乗 RBF => multiquadric
# 逆二乗 RBF => inverse
# 多重調和スプライン RBF => cubic(3次), quintic(5次), thin_plate(薄板スプライン)
# カーネルの種類配列作成
kernel = np.array(['linear', 'gaussian', 'multiquadric', 'inverse', 'cubic', 'quintic', 'thin_plate'])
# グラフの作成
plt.figure(figsize=(10, 8))
for i in range(len(kernel)):
# RBF 関数の作成
rbf = interpolate.Rbf(x, y, function=kernel[i])
# 入力されている x 値の最小値から最大値の間で任意の間隔で分割する
xi = np.linspace(x.min(), x.max(), 314)
# xi に対応する yi を計算する
yi = rbf(xi)
# グラフ描画
plt.plot(xi, yi, label='rbf - ' + kernel[i])
# 格子の設定
plt.grid(which='major', color='black', linestyle='-')
plt.grid(which='minor', color='black', linestyle='-')
# 格子の設定
plt.xlim([xi.min(), xi.max()])
plt.ylim([yi.min()*1.4, yi.max()*1.4])
plt.title("interpolate rbf")
plt.legend(loc='upper right') # 凡例の位置設定
# グラフ出力
file_name = "interpolate rbf.jpg"
plt.savefig(file_name)
plt.show()
#==============================================================================
# テスト
#==============================================================================
# 値の準備 =====================================================================
N = 2**5 # サンプリング数
dt = 0.01 # サンプリング周期
ampl = np.array([ 2]) # 振幅
freq = np.array([ 1]) # 周波数
peri_axis = np.arange(0, N*dt, dt) # 周期軸
error = 0.01 # 誤差係数
for i in range(len(freq)):
if i==0:
origin_y = ampl[i] * np.sin(2*np.pi*freq[i]*peri_axis) # 入力波形
y = ampl[i] * np.sin(2*np.pi*freq[i]*peri_axis) + error * np.random.randn(N) # 誤差を与えた入力波形
else:
origin_y += ampl[i] * np.sin(2*np.pi*freq[i]*peri_axis) # 入力波形
y += ampl[i] * np.sin(2*np.pi*freq[i]*peri_axis) + error * np.random.randn(N) # 誤差を与えた入力波形
# 補間 & 出力 =================================================================
rbf2d(peri_axis, y, 'linear')
rbf2d(peri_axis, y, 'gaussian')
rbf2d(peri_axis, y, 'multiquadric')
rbf2d(peri_axis, y, 'inverse')
rbf2d(peri_axis, y, 'cubic')
rbf2d(peri_axis, y, 'quintic')
rbf2d(peri_axis, y, 'thin_plate')
graph(peri_axis, y)
結果
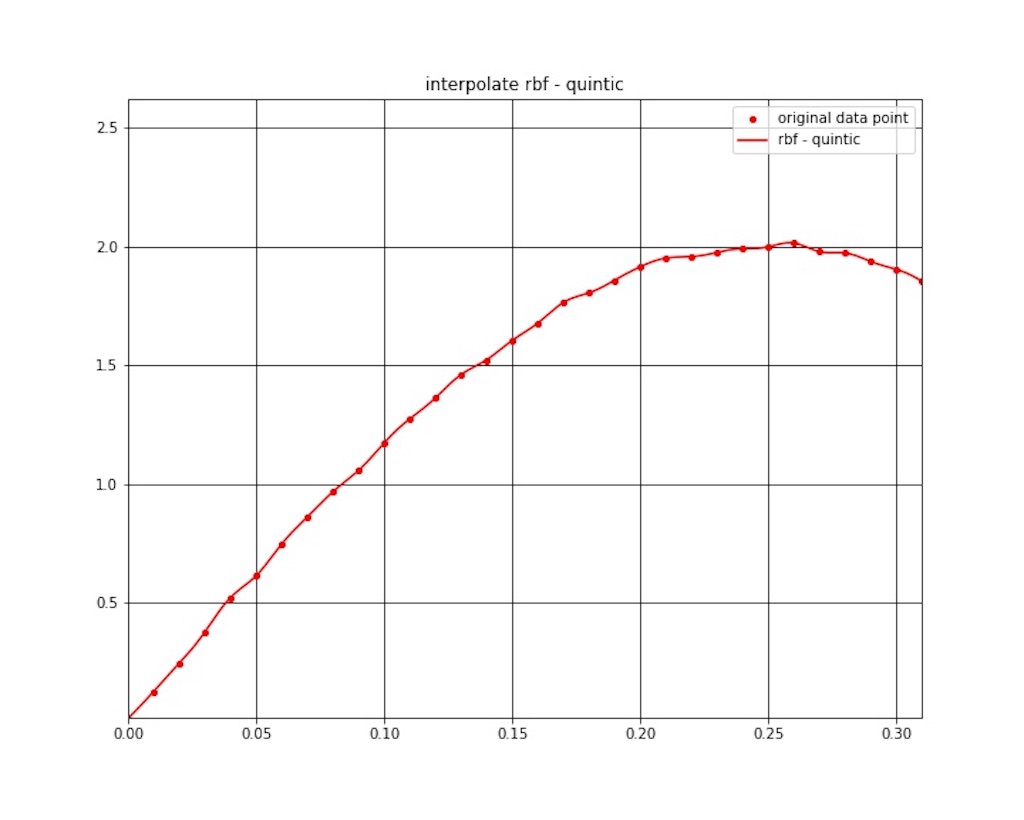
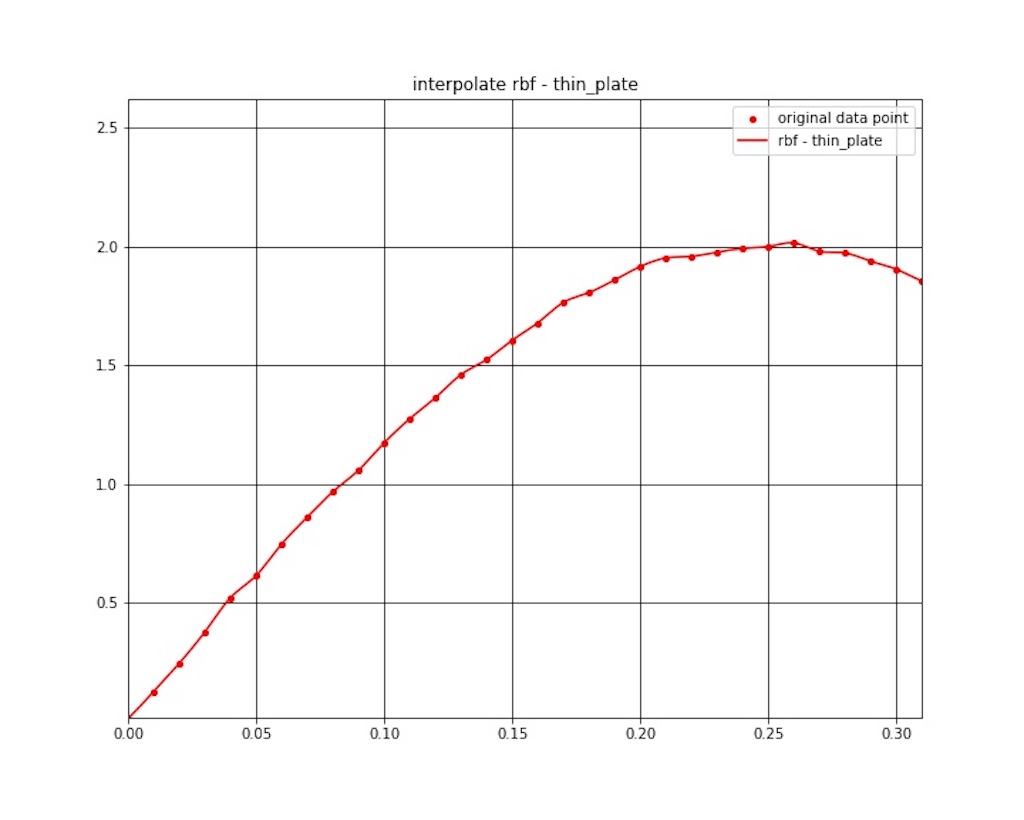
放射基底関数 (RBF) 補間の結果を図1 〜 図7 に示します。
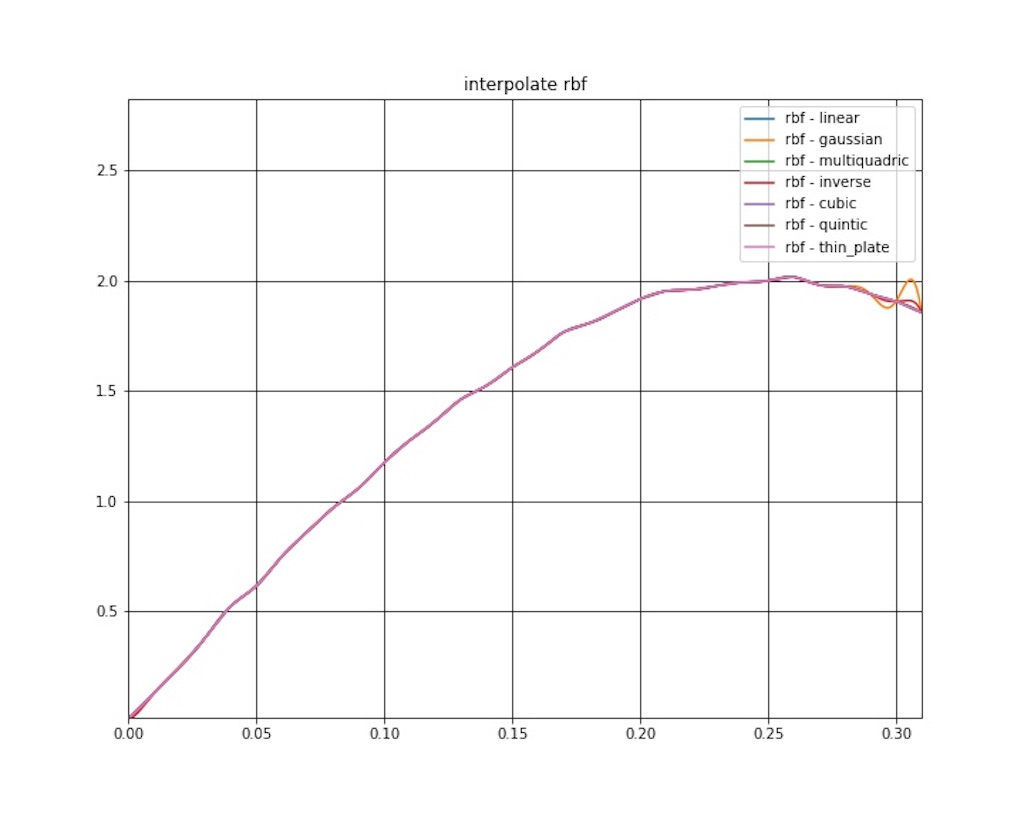
また、全てを重ね合わせた結果を図8 に示します。

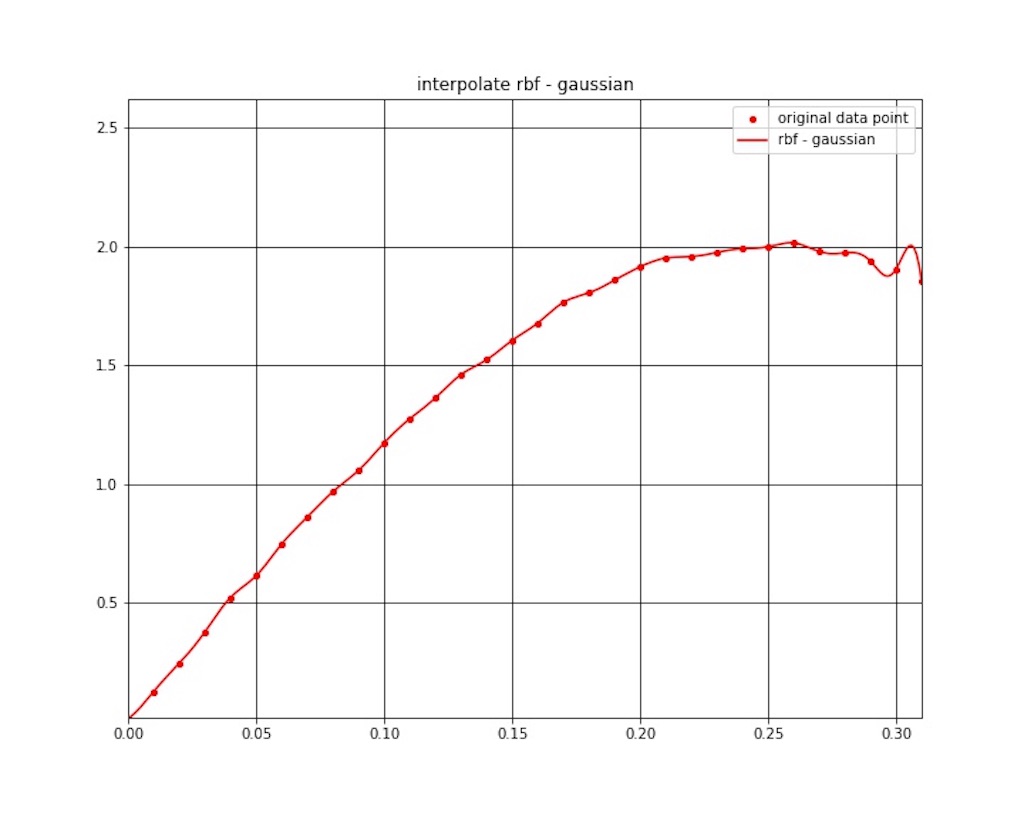
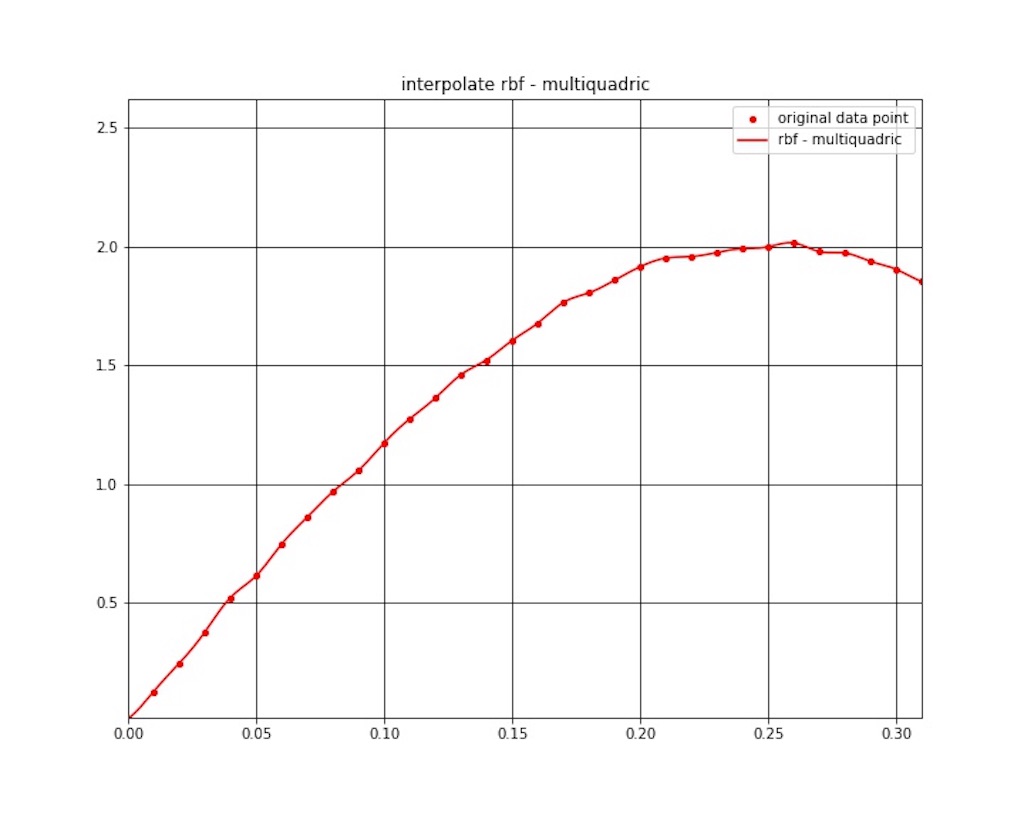
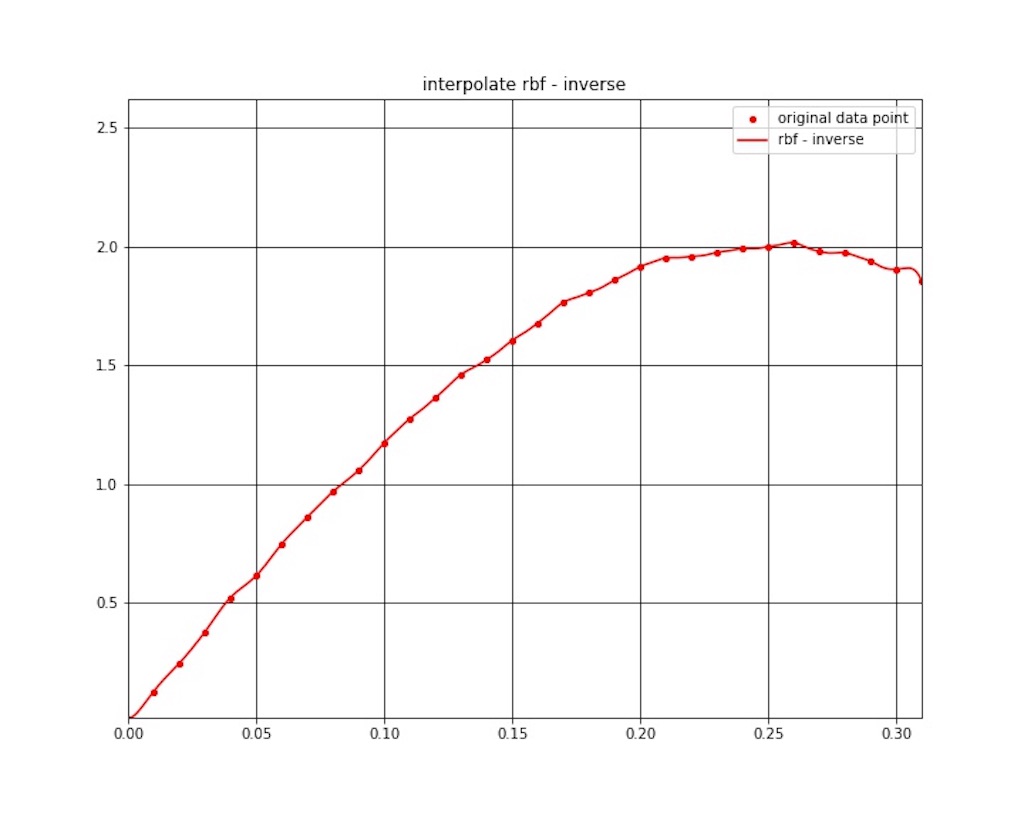
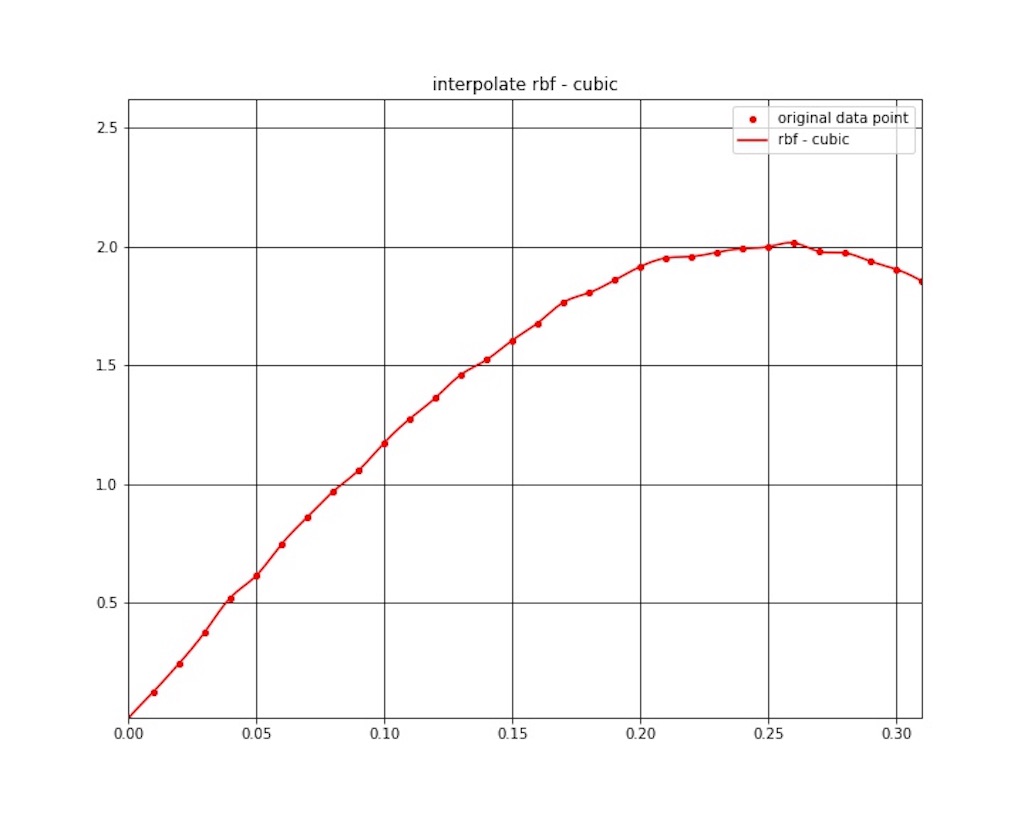
コメント
補間結果ですが、若干振動してますね。
ガウシアンがわりと大きく振動しててなんかショックでした。
自動でノイズ除去をして、自動でスプラインや放射基底関数 (RBF) 補間を選択して、自動で補間してキレイな波形データが得られる様になったら、良いんですけどね…
曲面の補間もやってみたいですね。
以上